Berekening van die Buigkrag tydens Vry Buig van Plaatmetaal Buigmasjien

In onlangse jare is metaalrembuigmasjiene wyd gebruik in verskeie nywerhede, en die verwerkingsreeks van buigmasjiene het uitgebrei. Daar was egter nie 'n sistematiese bespreking oor die berekening van buigkrag nie. Tans is daar rofweg twee tipes buigkragberekeningsformules wat aanbeveel word in die handleidings van verskeie vervaardigers van drukrembuigmasjiene.

P - buigkrag, KN;

S - plaatdikte, mm;

l - die buiglengte van die plaat, m;

V - die breedte van die onderste matrijsopening, mm;

σb - Materiaal treksterkte, MPa.

Die buigkragparametertabel wat deur die vervaardiger aanbeveel word, word ook volgens die bogenoemde formule bereken.

Die afleidingsproses en toepassingsomvang van buigkragberekeningsformule

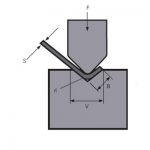
Figuur 1 is 'n skematiese diagram van die werk tydens plaatbuiging. Die volgende beskryf die afleidingsproses van die buigkragberekeningsformule en twee addisionele parametertoestande. Eerstens is daar sulke aanbevelings in die produkhandleiding. In vrye buiging is die geselekteerde onderste matrysopeningwydte V 8 tot 10 keer die plaatdikte S. Hier neem ons die aspekverhouding.

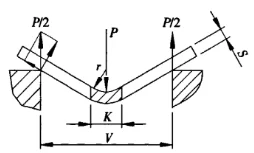
Figuur 1 Skematiese diagram van buiging

P - buigkrag

S - plaatdikte

V - laer matrysopeningwydte

r - die binneradius wanneer die plaat gebuig is

K - die breedte van die horisontale projeksie van die buigvervormingsone=9

Tweedens lys die vervaardiger die ooreenstemmende waardes van die matryswydte V en die binnedeursnee r van die buigwerkstuk op die buigkragparametertabel. Oor die algemeen r=(0.16~0.17)V. Hier is die deursnee-tot-breedte verhouding =0.16.

Tydens die buigproses van die plaatmetaal is die materiaal in die vervormingsone in 'n hoogs plastiese vervormingstoestand, en dit word teen 'n hoek om die middellyn gebuig. Op die buitenste oppervlak van die buigsone kan mikrokrake in sommige gevalle voorkom. Op die deursnee van die vervormingsone, behalwe vir die omgewing van die sentrale laag, is die spanning by ander punte naby aan die treksterkte van die materiaal. Die boonste deel van die neutrale laag word saamgepers en die onderste deel word gespan. Figuur 2 toon 'n deursnee en ooreenstemmende spanningsdiagram in die vervormingsone.

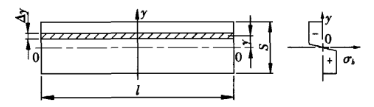
Figuur 2 Spanningsdiagram

S - plaatdikte

l - plaat buig lengte

Die buigmoment op die deursnee van die vervormingsone is:

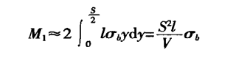
Die buigmoment wat deur die buigkrag van die masjien in die vervormingsone gegenereer word, is (sien Figuur 1):

Van

Wanneer algemene vormvorms vir vrye buiging op 'n buigmasjien gebruik word, word die meeste van die plaatmetaal 90° gebuig. Soos getoon in Figuur 3. K is:

Deur K in vergelyking (1) te vervang, kry ons:

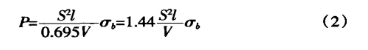
Die treksterkte van gewone materiale σb=450N/mm2, deur formule (2) te vervang in:

Uit die afleidingsproses kan gesien word dat wanneer vergelyking (2) of vergelyking (3) gebruik word om die buigkrag te bereken, die twee bykomende

parameter voorwaardes hierbo genoem moet nagekom word. Dit wil sê die aspekverhouding=9, die deursnee-tot-breedte verhouding=0.16, anders sal dit 'n groot fout veroorsaak.

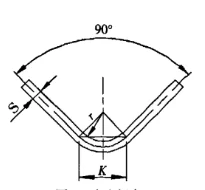
Figuur 3 Vrye buiging

S - plaatdikte

r - die binneradius wanneer die plaat gebuig is

K - die breedte van die horisontale projeksie van die buigvervormingsone

Nuwe metodes en stappe vir die berekening van buigkrag

As gevolg van ontwerp- of prosesvereistes is dit soms moeilik om tegelyk aan bogenoemde twee bykomende vereistes te voldoen. Op hierdie tydstip moet die aanbevole berekeningsformule nie gebruik word om die buigkrag te bereken nie, maar moet volgens die volgende stappe uitgevoer word.

(1) Volgens die plaatdikte S, die buigradius r, en die onderste matrijsopening V, word die breedte tot dikte verhouding en die deursnee tot breedte verhouding onderskeidelik bereken.

(2) Bereken die projeksiewydte van die vervormingsone volgens die vervorming van die plaat.

(3) Pas formule (1) toe om die buigkrag te bereken.

In die berekeningsproses is die verskil van die buigradius en die verandering van die ooreenstemmende vervormingsone in ag geneem. Die buigkrag wat hieruit bereken word, is meer akkuraat en betroubaar as die resultaat wat deur die gewoonlik aanbevole formule bereken word. Gee nou 'n voorbeeld om te illustreer, soos in Figuur 4 getoon.

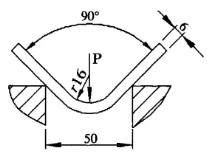
Figuur 4 Nuwe berekeningsmetode

Bekend: Die plaatdikte S=6mm, die plaatlengte l=4m, die buigradius r=16mm, die onderste matrysopeningwydte V=50mm, en die materiaaltreksterkte σb=450N/mm2. Vind die buigkrag wat benodig word vir vrye buiging.

Vind eers die aspekverhouding en deursnee-tot-breedte-verhouding:

Tweedens, bereken die projeksiewydte van die vervormingsone:

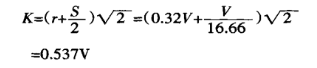
Ten slotte, gebruik vergelyking (1) om die buigkrag te vind:

As die gewone aanbevole formule gebruik word om die buigkrag te bereken:

Van = 1.5, dit kan gesien word dat die verskil tussen die twee 1.5 keer is. Die rede vir hierdie fout is dat die buigradius in hierdie voorbeeld relatief groot is, en die ooreenstemmende vervormingsarea word vergroot, dus 'n groter buigkrag word benodig tydens buiging. In hierdie voorbeeld is die deursnee-tot-breedte-verhouding=0.32, wat die bykomende voorwaardes van die parameters wat hierbo ingestel is oorskry het. Dit is natuurlik onvanpas om die gewoonlik aanbevole formule te gebruik om die buigkrag te bereken. U kan die voordele van die nuwe berekeningsmetode uit hierdie voorbeeld sien.

Afsluiting

Die stappe en formules vir die berekening van die buigkrag wat hier ingestel is, is nie net van toepassing op die hoekbuiging van plaatmetaal nie, maar ook van toepassing op die boogbuiging (streng gesproke moet dit die hoekbuiging met 'n ekstra groot buigradius genoem word). Daar moet daarop gewys word dat die vorm van die vorm spesiaal is wanneer die plaat in 'n boogvorm gebuig word. Wanneer die projeksie van die vervormingsone bereken word, moet dit bereken word volgens die tegnologiese parameters wat in die tegnologiese proses gestel is, wat nie deur 'n eenvoudige formule uitgedruk kan word nie.

Wanneer 'n boogvormige vorm ontwerp word, met behulp van die metode wat in hierdie artikel bekendgestel is om die buigkrag te bereken, kan bevredigende resultate verkry word.